プロスペクト理論について、一緒に考えてみたいと思います。
・損得の絶対量ではなく、変化量で価値を感じる
・実際の確率と感じ方に違いがある。
大きくとらえると、上記のような二大法則になります。
まず最初に、あなたが「5万円もらった時」と「5万円落として無くした時」どちらの感情が大きいでしょうか。
「嬉しい」と「悲しい」で真逆ですが、「5万円無くした時」の悲しさの方が感情が大きいのではないでしょうか。
確かに5万円を無条件にもらえたら嬉しいですが、自分の5万円無くしたら悲しいし、悔しいですよね!
1.プロスペクト理論とは
下のグラフを見てください。同じ5万円でも、もらった時と落とした時の価値(感情)の大きさが違うのです。
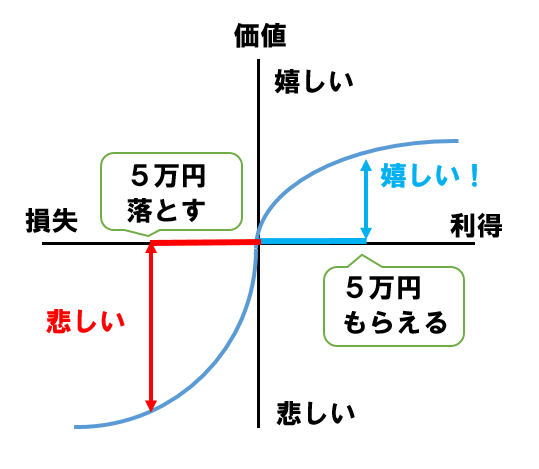
グラフは上に行くほど嬉しく、下に行くほど悲しい事を表しています。
同じ5万円を当てはめると「嬉しい」感情より、「悲しい」感情の方が大きくなっていますね。
2.25倍の差があるそうです。
単純に2倍として考えると、5万円落とした悲しみは10万円もらった時の嬉しさと同じという事です。
-5万円 = +10万円
と言われています。いかがですか?
人間は自分の保有するものを無くしたくないという(損失回避)の感情が大きいそうです。
それが金額の差にあらわれます。
損失回避は、次の例えも使われます。
2.プロスペクト理論とは?:参照点依存性
問題1:どちらを選びますか?
A:無条件に10万円もらえる。
B:じゃんけんで勝てば20万円もらえるが、負ければ何ももらえない。
あなたはAとB、どちらを選びますか?
もちろんBは「おあいこ」の時はやり直しですよ。
僕ならAを選び10万円もらいますが、いかがでしょう。
Bのじゃんけんの確率は50%ですので、20万円の50%となり期待値は10万円。
AとBの期待値の金額は10万円で同じですよね。
しかし多くの人がAを選ぶと思います。では次です。
問題2 :どちらを選びますか?
A:無条件に10万円没収される。
B:じゃんけんで勝てば没収されないが、負ければ20万円没収される。
この問題2はどちらを選びますか。
どちらも期待値は10万円です。
Bを選びませんか?50%の確率の没収されないことを願って!
問題1はAを選び、問題2はBを選ぶ。
もらう時と、失う時で違うのですよね。「損失回避」という、失う事を避けたいという心理からこのような結果になるのです。
もっと優しい事例
あなたがゲームの当事者です。下記のゲームを行いますか?
あなたがコインを投げます。
表が出たら、あなたは1万5千円もらえます。
裏が出たら、あなたは1万円支払います。
いかがでしょうか。このゲームをやりますか?
確率は50%ですが、1万5千円もらえるのです。支払いの1万円よりおおいですよ。
このゲーム、やらないですよね。
1万円支払いたくないですよね。(損失回避)です。
先ほどの2倍の感情の心理を考えると、
表なら2万円もらえて、裏なら1万円支払うのだったらいかがですか?
やってみようかな!ってなる人が多くなってくるのでしょう。
3.プロスペクト理論とは?:感応度逓減性
みなさん、ギャンブル好きですか?
パチンコ、競輪、競馬、宝くじ?
プロスペクト理論を、ギャンブルに当てはめてみます!
まずは意気揚々とパチンコはじめます!
あっさり1万円失ってしまいした。ショック、ガッカリです。
帰りますか?いえ、まだやります。しかしまた1万円失ってしました。
まだやりますか?もちろん、まだやります。取り返してやる!
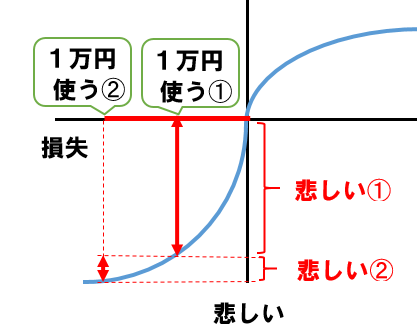
今、2万円失ったところです。
冒頭に出てきた図の左下を使います。
最初に使ったⅠ万円は➀、悲しみは➀
次に使ったⅠ万円は➁、悲しみは➁
2回目に使ったⅠ万円➁の悲しみは、➀の悲しみに比べてずいぶん少ないでしょう。
同じ1万円の損失なのに、1万円失う前と後では悲しい感情の大きさが全然違うのです。
悲しい感情がどんどん少なくなっていくので、お金をどんどん使ってしまうのですね。
ギャンブルの恐ろしさは、人間の心理からきているのです。
4.これもプロスペクト理論か?
社会人になり、先輩や上司と食事や飲み会に行きますよね。
2人の場合は奢ってもらったりしましたが、人数が多くなると金額的に厳しいですよね。
例えば、5人でお昼にラーメン屋さんに行ったとします。
1,000円/1人で、合計5,000円なり。
先輩が、

俺、3,000円出すよ!
残りをみんなで割って!

ごっさまでーす!
あざーす!

(俺、カッケー!)
心の中
5,000円-3,000円=2,000円を残りの4人で割ると、500円/1人ですね。
後輩たちは、1,000円のところ500円になります。
こういう奢られ方をされたことあったのですが、

1,000円が500円かー
あまり嬉しくないな。
500円奢ってもらったのですが、たいして嬉しくないのですよね。
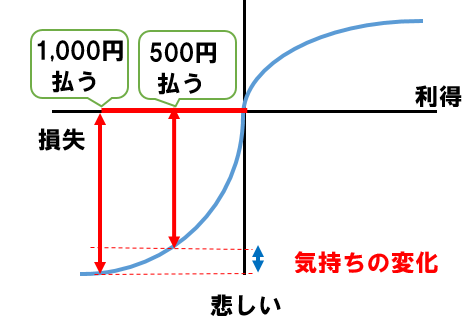
上記のようにプロスペクト理論に当てはめると、
1,000円払うつもりでいたところ、500円になった。気持ちの変化としては大きな差が無い。残念です。
唐突ですが、ラーメンが食べたくなったら「ラーメンの女帝」の記事を読んでみて下さい。
美味しそうなラーメンの写真の「どアップ」があります。
500円の牛丼を食べた時に、全額奢るようにした方が喜ばれるという事でしょうか。
下記のように気持ちの変化が大きいですよね。
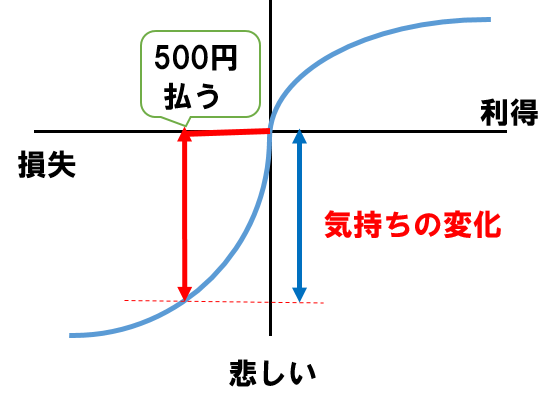
500円が0円になる方が嬉しいですよね!
次はもう一つの理論である確率加重関数のお話です。
5.プロスペクト理論の例:確率加重関数
みなさん宝くじを買ったことありますか。
僕は年末ジャンボなど、期待を込めて買ってしまう事があります。
一等の確率は1000万分の1=0.00001%のようです。
三等でも100万分の1。
一等を当てるには、上手く買って30億円分買えばいいことになります。
極端な話ですが、確率が低い時は人間は確率を高く感じてしまうそうです。
だから宝くじのように当たる確率が相当低くても、買ってしまうのですね。
では逆に確率が高い場合を考えてみましょう。
予防接種の重大な副反応などはいかがでしょうか。
重大な副反応が起きない確率が99.99%以上であったとしても、確率を低く見積もって心配になってしまうのですね。
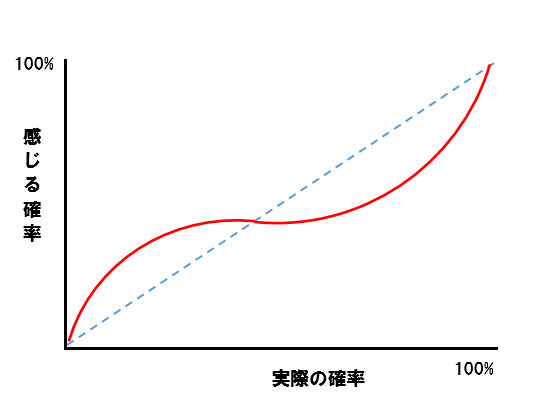
グラフの直線の破線に対して、赤の曲線が感じる確率です。
確率が低い時は高く感じ、確率が高い時は低く感じてしまうのです。
実際の確率と、感じる確率が一致しないという事です。
6.プロスペクト理論をビジネスに活用する
ビジネスではあらゆるところに活用されております。
「今日注文すれば、○○がついてきます!」
「ポイントが明日失効します!」
など損失を煽るのですよね。
会社内で使う
例えば新しい事業提案がなかなか通らない時、
「これを実現させれば、○○億円利益がでます。」
ではなく、「これをやらなければ○○億円損失します。」
このような、損失を報告してみてはいかがでしょうか。
その他にも、「この設備を導入すれば、年間100万円の効率化が見込めます!」
ではなく、「この設備を導入しなければ、年間100万円損失します!」という方が効果がありますね。
実践してみましょう!
Amazonの最新ビジネス書ランキングです。
こちらは楽天市場の最新ビジネス書ランキングです。
| 楽天市場 |
| 1位 |
| 2位 |
| 3位 |
| 4位 |
| 5位 |
| 資格取得などは省いています! |











コメント